Hai mặt phẳng vuông góc
Hai mặt phẳng vuông góc là kiến thức quan trọng trong chương trình Toán 11, các dạng bài tập liên quan tới 2 mặt phẳng vuông góc thường xuyên xuất hiện trong đề thi học kì, thi tốt nghiệp THPT. Hãy cùng VUIHOC tham khảo!

Định nghĩa hai mặt phẳng vuông góc
Hiểu đơn giản, hai mặt phẳng vuông góc là 2 mặt phẳng có góc giữa chúng bằng 90 độ.
Điều kiện để 2 mặt phẳng vuông góc
Hai mặt phẳng vuông góc với nhau khi và chỉ khi một mặt phẳng có chứa đường thẳng vuông góc với mặt phẳng còn lại
Các tính chất của hai mặt phẳng vuông góc
Trong trường hợp nếu 2 mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến của 2 mặt phẳng thì sẽ vuông góc với mặt phẳng kia.
Nếu hai mặt phẳng (A), (B) vuông góc với nhau và thì đường thẳng a qua điểm H (với điểm H nằm trên mặt phẳng A) và vuông góc với (B) sẽ nằm trong (A).
Nếu hai mặt phẳng cắt nhau và 2 mặt phẳng này cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng còn lại.
Hai mặt phẳng vuông góc trong tọa độ không gian Oxyz
Phương trình tổng quát của mặt phẳng (P) trong không gian tọa độ Oxyz có dạng tổng quát như sau:
Ax+By+Cz+D=0
với A2 + B2 + C2 > 0
Như vậy, để viết được phương trình mặt phẳng trong không gian, các em học sinh phải cần phải xác định được 2 dữ kiện:
- Điểm M nằm trên mặt phẳng
- Vector pháp tuyến của mặt phẳng
Đăng ký ngay để được các thầy cô tư vấn và xây dựng lộ trình ôn thi THPT môn Toán sớm ngay từ bây giờ
Điều kiện để hai mặt phẳng vuông góc trong không gian tọa độ Oxyz
Cho 2 mặt phẳng có phương trình lần lượt là:
(P):Ax+By+Cz+D=0
(Q):A′x+B′y+C′z+D′=0.
Điều kiện để 2 mặt phẳng vuông góc với nhau khi và chỉ khi thỏa mãn điều kiện: AA′+BB′+CC′+DD′=0.
Phương pháp chứng minh hai mặt phẳng vuông góc
Phương pháp chứng minh 2 mặt phẳng vuông góc với nhau
Cách 1: Chứng minh mặt phẳng này chứa đường thẳng (d) vuông góc với mặt phẳng còn lại.
Cách 2: Chứng minh góc giữa 2 mặt phẳng là 90 độ
Phương pháp chứng minh đường thẳng d vuông góc với mặt phẳng (α)
Cách 1: Nếu hai mặt phẳng cho trước cùng vuông góc với mặt phẳng thứ ba thì giao tuyến (nếu có) của chúng cũng sẽ vuông góc với mặt phẳng này.
Cách 2: Nếu 2 mặt phẳng vuông góc với nhau, nếu có một đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến của 2 mặt phẳng thì vuông góc với mặt phẳng còn lại.
Kết quả:
- S′=Scosφ
- Nếu hai mặt phẳng (Q) và (P) vuông góc với nhau, một điểm A bất kì thuộc mặt phẳng (P) thì mọi đường thẳng qua điểm A và vuông góc với mặt phẳng (Q) đều nằm trong mặt phẳng (P).
Tham khảo ngay bộ tài liệu nắm trọn kiến thức và phương pháp giải mọi dạng bài tập độc quyền của VUIHOC
Bài tập hai mặt phẳng vuông góc cơ bản
Bài tập tự luận
Bài tập 1: Cho hình chóp SABC có đáy là tam giác vuông ABC, góc B bằng 90 độ. Gọi 2 điểm H, K lần lượt là các hình chiếu vuông góc của A trên 2 đoạn thẳng SB, SC. Hãy chứng minh: mặt phẳng (SAB) vuông góc với mặt phẳng (SBC), mặt phẳng (AHK) vuông góc với mặt phẳng (SBC).

Hướng dẫn phương pháp giải
Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC):
Để chứng minh 2 mặt phẳng vuông góc với nhau, ta cần chứng minh trong mặt phẳng này có 1 đường thẳng vuông góc với mặt phẳng kia.
Ta có: Tam giác ABC vuông tại B
Suy ra: AB ⊥ BC (1)
SA ⊥ (ABC) ⇒ SA ⊥ BC (2)
Từ (1) và (2) ta suy ra được:
⇒ BC ⊥ (SAB), BC ⊂ (SBC) ⇒ (SAB) ⊥ (SBC) (điều phải chứng minh)
Chứng minh mặt phẳng (AHK) vuông góc với mặt phẳng (SBC)
Ta có:
BC ⊥ (SAB) mà AH thuộc mặt phẳng (SAB) ⇒ BC ⊥ AH(3)
H là hình chiếu vuông góc của A (theo giả thuyết)
⇒ SB ⊥ AH(4)
Từ (3) và (4) ta suy ra được
AH ⊥ (SBC) mà AH ⊂ (AHK) ⇒ (AHK) ⊥ (SBC) (điều phải chứng minh)
Bài tập 2: Cho hai mặt phẳng Δ và (β) vuông góc với nhau và cắt nhau thông qua giao tuyến d. Hãy chứng minh nếu có một đường thẳng Δ nằm trong Δ và Δ vuông góc với giao tuyến d thì Δ vuông góc với mặt phẳng (β).

Hướng dẫn phương pháp giải
Ta có:
Từ điểm A, ta kẻ đường thẳng a:
Do hay
Bài tập trắc nghiệm
Bài tập số 1: Cho tứ diện ABCD có AB ⊥ (BCD) . Trong tam giác BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?
A. (ADC) ⊥ (ABE) B. (ADC) ⊥ (DFK)
C. (ADC) ⊥ (ABC) D. (BDC) ⊥ (ABE)

Hướng dẫn giải
Ta xét các phương án mà đề bài ả:
- Ta có:
CD BE
CD AB
=> CD (ABE) mà CD
(ADC) => (ADC)
(ABE) => Đáp án A đúng
- DF
BC; DF
AB => DF
(ABE)
mà SC (ABC)
=>
Vậy (ADC) (DFK) => Vậy đáp án D đúng
- Ta có:
Tương tự ta có thể chứng minh được đáp án C sai
Vậy đáp án C
Bài tập số 2: Cho tứ diện ABCD với hai mặt phẳng (ABC) và (ABD) cùng vuông góc với mặt phẳng (DBC) . Gọi DF và BE lần lượt là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Trong các khẳng định dưới đây, khẳng định nào là sai
A. (ABE) ⊥ (ADC) B. (ABD) ⊥ (ADC)
C. (ABC) ⊥ (DFK) D. (DFK) ⊥ (ADC)
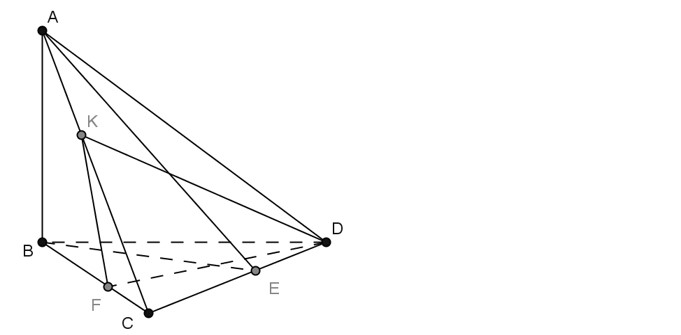
Hướng dẫn giải

Vậy đáp án lựa chọn là đáp án B
PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA
Khóa học online ĐẦU TIÊN VÀ DUY NHẤT:
⭐ Xây dựng lộ trình học từ mất gốc đến 27+
⭐ Chọn thầy cô, lớp, môn học theo sở thích
⭐ Tương tác trực tiếp hai chiều cùng thầy cô
⭐ Học đi học lại đến khi nào hiểu bài thì thôi
⭐ Rèn tips tricks giúp tăng tốc thời gian làm đề
⭐ Tặng full bộ tài liệu độc quyền trong quá trình học tập
Đăng ký học thử miễn phí ngay!!
Trên đây là toàn bộ lý thuyết về hai mặt phẳng vuông góc. Hy vọng với bài viết trên sẽ giúp các em có thể nắm chắc được kiến thức và có thêm các phương pháp giải các dạng bài tập liên quan tới mặt phẳng trong chương trình toán 11 cũng như trong quá trình ôn thi tốt nghiệp THPT môn Toán. Để tham khảo thêm kiến thức của các môn khác, các em học sinh có thể truy cập vuihoc.vn. Chúc các em đạt được điểm cao trong kì thi sắp tới.
Tham khảo thêm:
⭐Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết
Bài viết tham khảo thêm:

















