Tổng Hợp Các Dạng Phương Trình Lượng Giác Thường Gặp
Trong chương trình toán THPT, các em sẽ được làm quen với dạng bài về phương trình lượng giác thường gặp. Bài viết dưới đây Vuihoc.vn sẽ tổng hợp đầy đủ về phương trình lượng giác thường gặp cùng ví dụ minh họa giúp các em hiểu bài nhanh hơn.

1. Phương trình bậc nhất đối với hàm số lượng giác sinx và cosx
Phương trình bậc nhất với một số hàm số lượng giác có dạng phương trình như sau:
at+b=0
Trong đó:
+ a,b: hằng số (a≠0)
+ t: một trong các hàm số lượng giác
Phương trình lượng giác dạng:
asinx+bcosx=c
Trong đó: có a,b,c cùng thuộc R, $a^{2}+b^{2}\neq 0$ là phương trình bậc nhất với sinx và cosx.
Ta xét:
+ Nếu $a^{2}+b^{2}< c^{2}$ thì phương trình vô nghiệm.
+ Nếu $a^{2}+b^{2}\geqslant c^{2}$, để tìm nghiệm của phương trình ta thực hiện tiếp các bước sau.
Với phương trình bậc nhất đối với hàm số lượng giác sinx và cosx, ta xét phương trình asinx+bcosx=c
Lúc này:
+ Ta chia 2 vế của phương trình cho $\sqrt{a^{2}+b^{2}}$
+ Gọi $\alpha$ là góc lượng giác được tạo ra bởi chiều dương của trục hoành với vectơ $\vec{OM}=(a,b)$, phương trình trở thành:
$sin(x+\alpha )=\frac{c}{\sqrt{a^{2}+b^{2}}}$ (1)
Điều kiện phương trình có nghiệm:
$\left | \frac{c}{\sqrt{a^{2}+b^{2}}} \right |\leqslant 1 \Rightarrow \left | c \right |\leqslant \sqrt{a^{2}+b^{2}} \Rightarrow c^{2}\leqslant a^{2}+b^{2}$
Suy ra được điều kiện để phương trình asinx +bcosx = c có nghiệm
Công thức đặc biệt:
• sinx+cosx=0
⇔x= –π4+kπ (k∈Z).
• sinx–cosx=0
⇔x=π4+kπ
Ví dụ: Hãy giải phương trình sau: (1+$\sqrt{3}$)sinx + (1-$\sqrt{3}$)cosx=2
Giải:
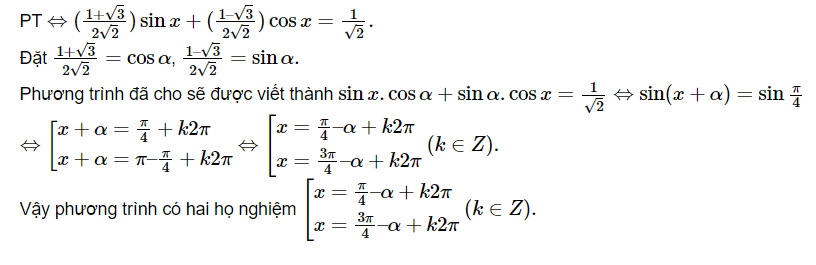
2. Phương trình bậc hai một số hàm lượng giác
Dạng 1: $asin^{2}x+bsinx+c$ (a≠0;a,b,c∈R)
Phương pháp giải:
Đặt:
- t=sinx, với điều kiện |t|≤1, sau đó đưa phương trình $asin^{2}x+bsinx+c$ về phương trình bậc hai theo t.
- Giải phương trình tìm ra t, chú ý kết hợp điều kiện của t rồi tìm x.
Dạng 2: $acos^{2}x+bcosx+c$, (a≠0; a,b,c∈R).
Phương pháp giải: Đặt t=cosx, điều kiện |t|≤1
- Đưa phương trình $acos^{2}x+bcosx+c$ về phương trình bậc hai theo t.
- Giải phương trình ra tìm t, chú ý kết hợp điều kiện của t rồi tìm x.
Dạng 3: $atan^{2}x+btanx+c$ (a≠0; a,b,c∈R).
Phương pháp giải: Điều kiện cosx≠0
⇔x≠π2+kπ (k∈Z).
- Đặt t=tanx (t∈R), đưa phương trình $atan^{2}x+btanx+c$ về phương trình bậc hai theo t. Chú ý rằng khi tìm được nghiệm x cần thử lại vào điều kiện xem có thoả mãn hay không.
Dạng 4: $acot^{2}x+bcotx+c$ (a≠0; a,b,c∈R).
Phương pháp giải: Điều kiện sinx≠0 ⇔x≠kπ (k∈Z).
-
Đặt t=cotx (t∈R), ta đưa phương trình $acot^{2}x+bcotx+c$ về phương trình bậc hai theo ẩn t
-
Giải ra t rồi tìm x, chú ý khi tìm được nghiệm cần thử lại vào điều kiện xem có thoả mãn hay không.
Ví dụ: Hãy giải phương trình $2cos^{2}x-3cosx+1$
Giải:

Đăng ký ngay khóa học DUO 11 để được các thầy cô ôn tập kiến thức và xây dựng lộ trình ôn thi tốt nghiệp THPT môn Toán ngay từ bây giờ
3. Phương trình lượng giác thuần bậc hai đối với sinx và cosx
Phương trình thuần nhất bậc hai với sinx và cosx là phương trình có dạng: $asin^{2}x+bsinx.cosx+ccos^{2}x=d$, trong đó có: a,b,c,d cùng thuộc R.
Phương pháp giải:
Ta chia từng vế của phương trình cho một trong ba $sin^{2}x$, $cos^{2}x$ hoặc sinx.cosx. Ví dụ nếu ta chia cho $cos^{2}x$ ta làm theo các bước sau:
-
Cho: cosx=0 ⇔x=2 + kπ (k∈Z) xem nó có phải là nghiệm của phương trình $asin^{2}x+bsinx.cosx+ccos^{2}x=d$ không?
-
Với cosx≠0, chia cả hai vế cho $cos^{2}x$, lúc này phương trình $asin^{2}x+bsinx.cosx+ccos^{2}x=d$ trở thành: $atan^{2}x+btanx+c=d(1+tan2x)$
⇔ $(a-d)tan^{2}x+btanx+c-d=0$.
Ta xét thấy, phương trình có dạng bậc hai theo tan.
Ví dụ: Hãy giải phương trình $2\sqrt{3}cos^{2}x+6sinxcosx=3+\sqrt{3}$

4. Phương trình đối xứng với sinx và cosx
Phương trình đối xứng với sinx và cosx là phương trình dạng a(sinx+cosx)+bsinxcosx+c=0, với a,b,c thuộc R.
Phương pháp giải:
Do: $(sinx+cosx)^{2}$
= 1+2sinx.cosx nên ta đặt:
t=sinx+cosx= $\sqrt{2}sin(x+\frac{\pi }{4}) = 2cosz(\frac{\pi }{4}-x)$
Điều kiện |t|≤2.
Nên sinx.cosx = $\frac{t^{2}-1}{2}$ và phương trình a(sinx+cosx)+bsinxcosx+c=0 được viết lại là $bt^{2}+2at-(b+2c)=0$
Ví dụ: Giải pt sinx+cosx–2sinx.cosx+1=0
Giải:

Đăng ký ngay để được các thầy cô ôn tập kiến thức và xây dựng lộ trình ôn thi Toán THPT sớm đạt 9+
5. Phương trình lượng giác dạng thuận nghịch
Ta có dạng phương trình thuận nghịch là:
$A(f^{2}(x)+\frac{k^{2}}{f^{2}(x)})+B(f(x)+\frac{k}{f(x)})+C=0$ (1)
Hoặc $A(a^{2}tan^{2}x+b^{2}cot^{2}x)+B(atanx+bcotx)+C=0$ (2)
Giải:
-
Đối với (1): Đặt t=f(x) + $\frac{k}{f(x)}$
-
Đối với (2): Đặt t=a tanx + b cotx
Ví dụ: Giải phương trình $\frac{3}{cos^{2}x}+3cot^{2}x+4(tanx+cotx)-1=0$
Giải:

6. Phương trình đẳng cấp bậc hai đối với sinx và cosx
Phương trình đẳng cấp bậc 2 đối với sinx và cosx là phương trình có dạng:
$asin^{2}x+bsinx.cosx+ccos^{2}x=d$
Trong đó: x là một ẩn số
a,b,c,d là hệ số
Giải:
-
Trường hợp 1: a=d
Lúc này phương trình có dạng:
$asin^{2}x+bsinx.cosx+ccos^{2}x=a$
$\Leftrightarrow asin^{2}x+bsinx.cosx+ccos^{2}=asin^{2}x+acos^{2}x$
$\Leftrightarrow bsinx.cosx+(c-a)cos^{2}x=0$
$\Leftrightarrow cosx\left [ bsinx+(c-a)cosx \right ]=0$
$\Leftrightarrow cosx=0$ hoặc $[ bsinx+(c-a)cosx \right ]=0$
Trường hợp 2: $a\neq d$
$\Leftrightarrow asin^{2}x+bsinx.cosx+ccos^{2}x=dsin^{2}x+dcos^{2}x$
$\Leftrightarrow (a-d)sin^{2}x+bsinxcosx+(c-d)cos^{2}x=0$
Có thể thấy cosx=0 không phải là nghiệm phương trình, ta chia cả 2 vế cho cos^{2}x ta được:
$(a-d)tan^{2}x+btanx+c-d=0$
Ví dụ: Giải phương trình: $6sin^{2}x+14sinxcosx-4(1+cos2x)=6$
Giải:
PT $\Leftrightarrow 3(1-cos2x)+7 sin2x-4(1+cos2x)=6$
$\Leftrightarrow 7sin2x-7cos2x=7$
$\Leftrightarrow sin2x-cos2x=1$
$\Leftrightarrow sin(2x-\frac{\pi }{4})=\frac{1}{\sqrt{2}}$
$\Leftrightarrow x=\frac{\pi }{4}+k\pi$ hoặc $x=\frac{\pi }{2}+k\pi$
Tham khảo ngay một số dạng bài tập về lượng giác được các thầy cô VUIHOC tổng hợp
PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA
Khóa học online ĐẦU TIÊN VÀ DUY NHẤT:
⭐ Xây dựng lộ trình học từ mất gốc đến 27+
⭐ Chọn thầy cô, lớp, môn học theo sở thích
⭐ Tương tác trực tiếp hai chiều cùng thầy cô
⭐ Học đi học lại đến khi nào hiểu bài thì thôi
⭐ Rèn tips tricks giúp tăng tốc thời gian làm đề
⭐ Tặng full bộ tài liệu độc quyền trong quá trình học tập
Đăng ký học thử miễn phí ngay!!
Bài viết trên đã tổng hợp lý thuyết cũng như các dạng toán về phương trình lượng giác thường gặp. Hy vọng rằng các em sẽ tiếp thu bài học dễ dàng hơn và giải bài tập thật thành thạo. Truy cập ngay nền tảng học online Vuihoc.vn để để ôn tập nhiều hơn về các dạng bài tập khác thuộc chương trình Toán 11! Chúc các bạn ôn tập hiệu quả.
Tham khảo thêm:
⭐Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết
>> Bài viết tham khảo thêm:
















